协同编辑冲突处理算法综述【转】

1.主流协同冲突算法简介

在实时协同编辑系统领域，OT（Operational Transformation）算法核心原理基于操作转换，是最早（1989年）被提出的协同冲突处理算法，而后因为Google Wave应用流行起来。OT算法相关的研究如今得到了广泛的实际应用，例如Google Docs和腾讯文档，底层的协同冲突处理算法都是基于OT算法实现。

AST（Address space transformation）算法，最早于2005年提出，其核心思想是在执行操作前回溯文档生成操作时的状态，通过转换地址空间实现协同。在协同编辑学术领域，相关的研究成果不断在提出，不过现实中的实际应用较少。

CRDT (Conflict-free Replicated Data Type)即“无冲突复制数据类型”，最早正式于2011年提出，在分布式系统中，CRDT 是指一种可以在网络中多个主机中并行地复制的一种数据结构，副本可以独立和并发地更新，而不需要副本之间的协同。CRDT应用面非常广，不仅可用于协同编辑领域，还被用于在线聊天系统、NoSQL分布式数据库等。在协同编辑领域基于CRDT的冲突处理算法，例如 WOOT算法（WithOut OT），atom 编辑器的协同插件teletype即是基于WOOT实现。

本文将分别对这三种算法基本原理进行简单介绍。

2.相关基本概念和术语

2.1 交换律、结合律、幂等律

交换律 是被普遍使用的一个数学性质，意指能改变某物的顺序而不改变其最终结果。交换律是大多数数学分支中的基本性质，比如基本的加法运算即符合交换律： 1+2 = 2+1。

结合律 是二元运算可以有的一个性质，意指在一个包含有二个以上的可结合运算子的表示式，只要运算数的位置没有改变，其运算的顺序就不会对运算出来的值有影响。例如加法同样符合结合律：1 + 2 + 3 = 1 + （2 + 3）= 6。

幂等律 有两种主要的定义：

• 1.在某二元运算下，幂等元素是指被自己重复运算的结果等于它自己的元素。例如，乘法下唯一两个幂等实数为0和1，即1*1*1 = 1，0^N = 0。
• 2.某一元运算 f(x) 符合幂等律时，f(f(x)) = f(x) , 作用在任一元素两次后会和其作用一次的结果相同，一元运算的定义是二元运算定义的特例。

2.2 全序和偏序

偏序： 假设集合S 满足以下条件，则为满足偏序关系：
(1)自反性： 对S中任意的元素a，都有 a≤a.
(2)反对称性： 如果对于S中的两个元素 a 和 b， a≤b 且 b≤a，那么 a=b
(3)传递性： 如果对于S中的三个元素，有a≤b 且 b≤c， 那么 a≤c

全序 则比偏序的要求更为严格一些， 在偏序的基础上，多了一个条件：
(4)完全性： 对于S中的任意a、b元素，必然有 a≤b 或 b≤a.
全序就是在偏序的基础上，要求全部元素都必须可以比较。总结概括就是，偏序是部分可比较的序关系，全序是全部可比较的序关系。
下图1用有向图举例描述全序和偏序的区别：

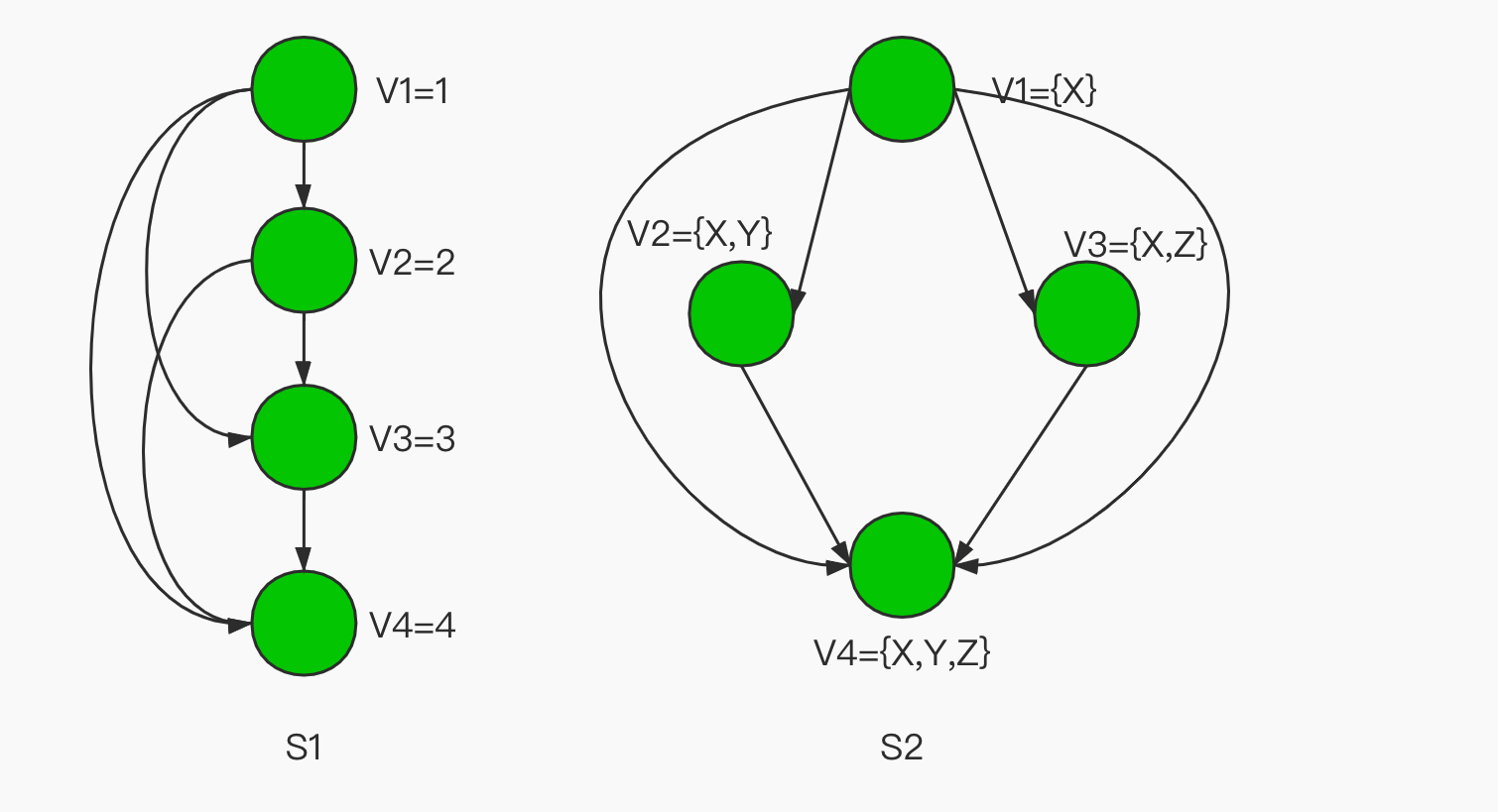
图1 全序和偏序示例

图1中S1描述的是整数之间的大小关系，是一种全序关系，任意两个元素都可以进行大小的比较；S2描述的是集合之间的包含关系，是一种偏序关系，其中V2和V3不存在包含关系，无法比较。
操作的全序是给实时协同编辑系统中产生的所有操作赋予唯一的全局次序, 这样即可以按照全序进行操作转换或按照全序执行.

2.3 因果关系、并发关系

基于偏序关系定义因果关系和并发关系。

假设当一个用户在站点1执行操作opA时，站点1上的操作可以分为三个部分：
(1)因果先序：执行操作opA时，在站点1上已经执行的操作集合｛X｝称为因果先序，表示为 X->opA
(2)因果后序： 操作opA到达其他站点后产生的操作和站点1本地在opA之后产生的操作｛X｝称因果后序操作，表示为 opA->X
(3) 并发操作：既不满足因果先序也不满足因果后序的操作 {X} 称并发操作，表示为 X||A

因果关系即表示opA、opB两个操作满足因果先序opA->opB或因果后序opB->opA；并发关系即表示opA||opB。
简单并发关系：满足并发关系的两个操作的产生基于相同的文档状态
偏并发关系：满足并发关系的两个操作的产生于不同的文档状态

2.4 一致性模型

协同冲突处理算法的功能其中之一是支持协同编辑系统的一致性维护，而在研究领域已经提出了许多一致性模型，比如CC模型、CCI模型、CSM模型、CA模型。这里举例说明下CCI模型，CCI模型由以下几个属性组成：

(1)收敛性(Convergence)：在执行所有操作后，同一文档的所有副本必须是相同的，即不同站点下文档的状态一致

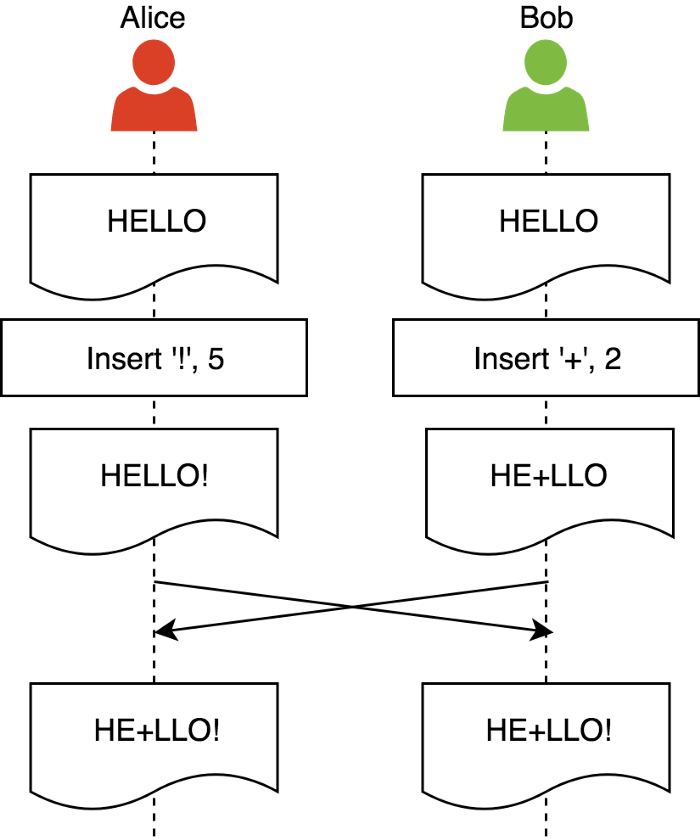
如图，Alice和Bob两人在不同站点同时对同一份文档进行了编辑操作，收敛性需要保证双方收到各自的更改后，两人最终能看到相同的文档结果。

(2)维护因果关系（Causality preservation）:在协同过程中，编辑操作必须按照自然的因果关系顺序来执行。通过下图的例子说明下：

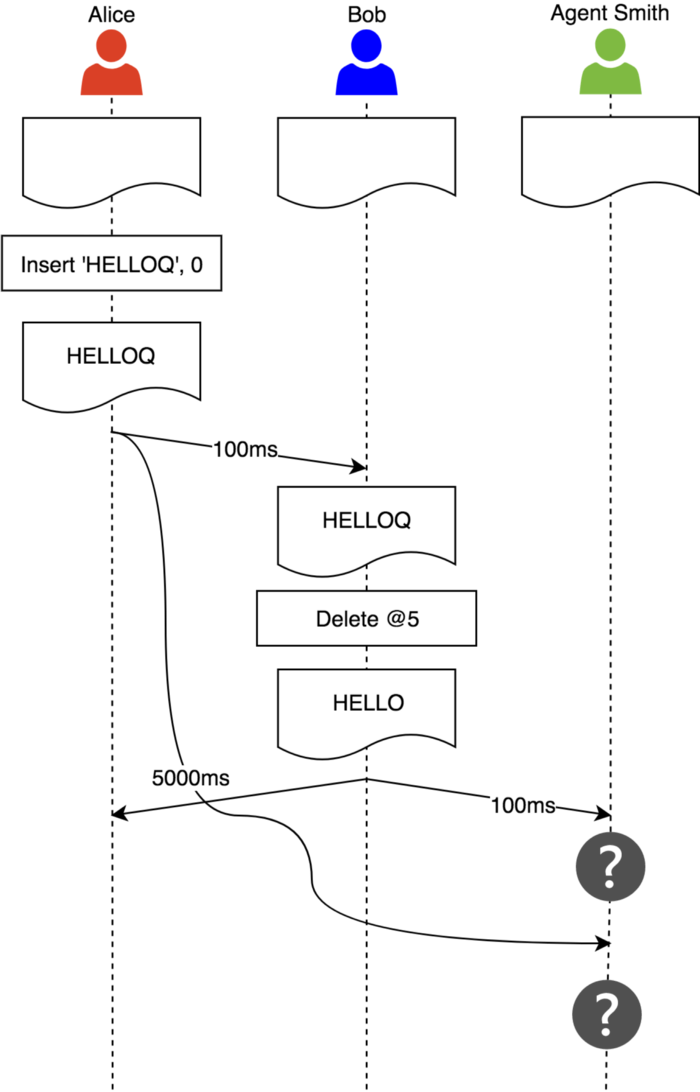
Alice,Bob和Agent Smith同时编辑同一份文档，Alice插入内容并同步给其他站点，Bob首先接收到Alice的内容然后删除修正了内容并同步给其他站点。由于网络延迟，Agent Smith首先收到了Bob的操作同步结果，而此时本地副本还没有内容可供删除。
原始的OT算法无法保证因果关系顺序，所以类似加入Vector clock数据结构的机制就被应用起来解决这个问题。

(3)保留意图（Intention preservation）：确保对任何文档状态执行操作的效果与操作的意图一致，操作的意图即用户对本地的副本文档进行编辑操作希望得到的结果。

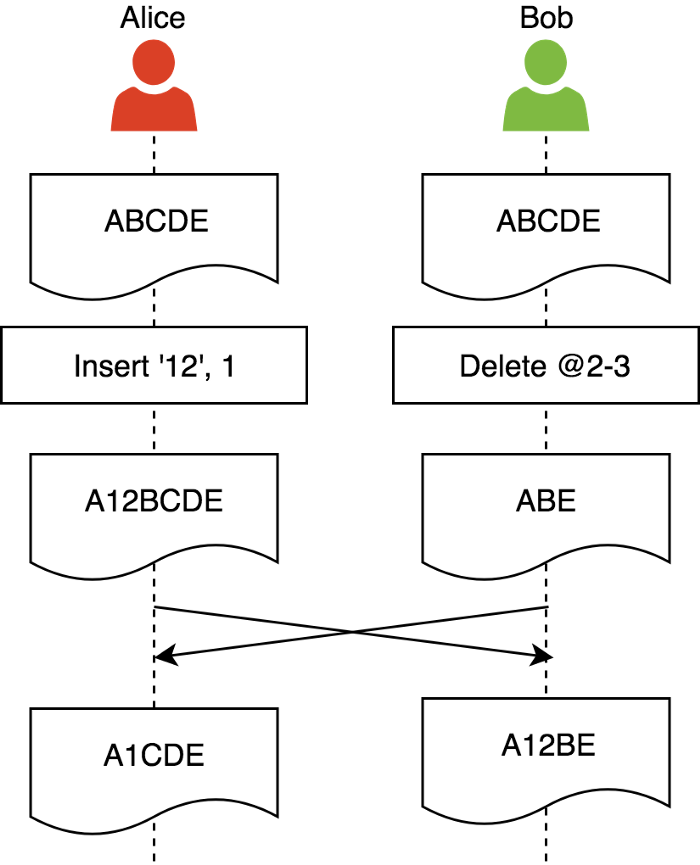
如上图，Alice和Bob对同一文档同时进行编辑操作，在未满足保留意图的情况下，Alice接收并直接同步Bob原始操作，所得到的结果是没有保留Alice操作意图的。

3. OT算法

3.1 OT算法简介

OT是一种基于操作转换的协同冲突处理算法，核心思想是对操作进行转换后应用到状态发生冲突的文档，让不同的协同端都能够到达一致的状态。

OT算法的工作原理大致可概括为：

• (1)文档的每次更改（插入或删除）都可以抽象表示为一个操作，每个操作都可以应用到文档中使文档产生一个新的文档状态。
• (2)为处理并发的文档编辑操作，通过转换方法将基于同一个文档状态的两个操作（操作来自不同站点）转换生成新的操作，将新的操作应用到两个操作之后执行使不同站点结果一致，且能保留两个操作的更改意图。

3.2 OT算法设计

3.2.1 OT算法系统架构

OT算法系统由多个部分组成。以一个确定的OT系统设计策略为例说明，OT算法的设计可分为三个部分：
(1)转换控制算法：负责确定操作何时进行转换，应该对哪些操作进行转换，以及应该以何种顺序进行转换。
(2)转换函数：负责根据操作类型、位置和其他参数转换一对目标操作
(3)性质和条件：定义转换控制算法和转换函数之间的关系

3.2.2 OT数据和操作模型

在OT算法系统中，有两个基本的模型：

• 数据模型：定义文档为数据对象，从而可以通过操作进行处理
• 操作模型：定义可以由OT转换函数直接转换的操作集,

不同的OT系统可能有不同的数据和操作模型。比如，原始的OT系统数据模型为一个线性的地址空间，操作模型由字符插入和字符删除两个基本操作组成。经过发展之后基本的操作模型已经扩展增加了第三类基本操作“更新” [1]，用于支持文档的冲突处理；基本的数据模型也扩展为多个线性寻址域的层次结构 [2]，用于对更加广泛类型的文档进行建模。设计数据模型后，通常还需要一个适配过程来将特定的应用程序数据模型映射到OT数据模型。

OT系统一般有两种操作模型：

• (1)通用操作模型：基于插入、删除、更新三种基本操作设计转换函数。此种方式需要将应用程序的操作抽象映射为三种基本的操作，这种OT操作模型是通用的，所有转换函数可以复用到其他应用。
• (2)特定应用操作模型：为应用程序的每一对操作设计转换函数，应用程序如果有m个不同的操作，那需要m*m个转换函数。此种操作模型为应用程序特定，不可复用到其他应用。

3.2.3 OT转换函数

OT转换函数可以分为两种类型：

• 包含/向前转换：IT(Oa,Ob) 转换操作Oa和操作Ob，使Ob的影响保留（如两个插入）
• 排除/向后转换：ET(Oa,Ob) 转换操作Oa和操作Ob，使Ob的影响失效（如插入之后删除）

有些OT系统同时应用IT和ET转换函数，有些只用IT转换。OT系统的设计复杂度由多种不同的因素决定：

• OT系统的功能：OT系统是否需要支持一致性维护、撤销、锁定、分享等
• OT系统的正确性：需要满足哪些转换性质（CP1/TP1,CP2/TP2等，解释见下节3.2.4);是否使用ET转换
• OT系统操作模型：OT系统的操作模型是通用的（插入、删除、更新），还是应用程序特定的
• OT系统数据模型：每个操作中的数据是字符，字符串还是分层或其他结构

3.2.4 转换性质

为了确保OT系统的正确性，确定了各种转换性质，这些性质通过转换控制算法和转换函数来维持。举例说明CP1/TP1和CP2/TP2两种收敛相关转换性质：

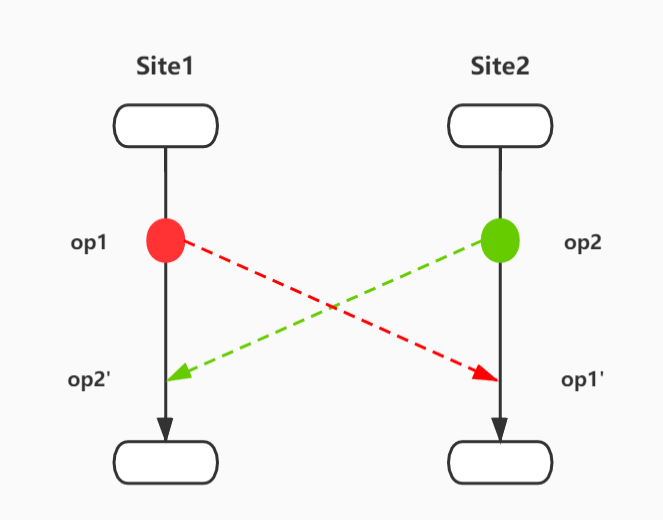
给定两个操作op1和op2,进行转换op1' = IT(op1,op2), op2' = IT(op2,op1)，转换函数IT需要满足以下两种与收敛有关的性质：

CP1/TP1：op1 o IT(op2,op1) = op2 o IT(op1,op2)
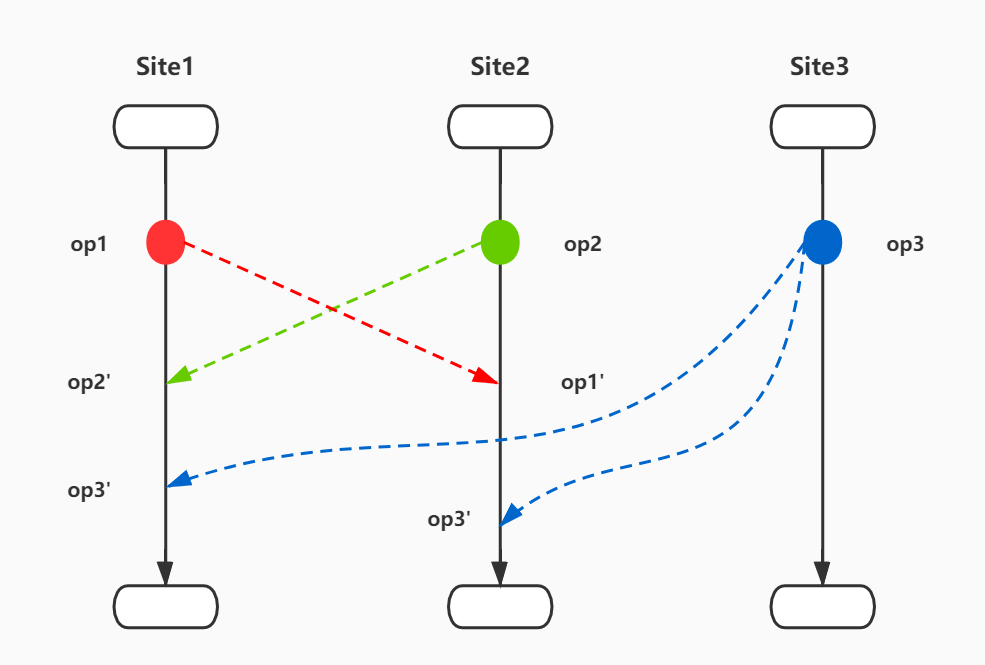
CP2/TP2: IT(op3, op1 o IT(op2,op1) ) = IT( op3, op2 o IT(op1, op2) )

以上表达式解释如下：CP1/TP1 保证基于同一文档状态的并发协同操作op1、op2，无论op1或op2谁先执行，结果一致；CP2/TP2 保证基于同一文档状态的并发协同操作op1、op2、op3，对于两个等价的操作序列，转换后的结果是相同的，即无论是操作序列op3->op1->op2'还是操作序列op3->op2->op1'转换后的操作op3'结果一致。图示如下：

CP1/TP1示例

CP2/TP2示例

3.2.5 OT转换控制算法

针对不同功能和应用的OT系统可以设计不同的OT控制算法，比如Google Wave的OT算法，其转换函数维持CP1/TP1性质且只使用IT转换，控制算法维持CP2/TP2性质。接下来以Google Wave的OT算法为例，介绍其转换控制过程：

1.数据模型

Google Wave数据模型的主要元素有：
Wave：每个Wave都有一个全局唯一的Wave ID，是一组Wavelet的集合。
Wavelet：Wavelet在其所属的Wave中有一个唯一ID，Wavelet由一个协同参与者列表和一组文档组成。Wavelet是并发控制/操作转换请求的实体。
文档：文档在其所属的Wave中有一个唯一ID，由一个类XML文档和一组“分离”注解组成。注解指向XML文档，不依赖于XML文档的结构，它们用来表示文本格式、拼写建议和超链接。文档在Wavelet中构成一棵树。

2.操作模型

在Google Wave中，文档中的每个字符、开始标记或结束标记称为一个节点，节点之间的间隙称为位置，位置0在第一个节点之前。示意图如下：

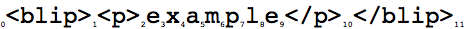
文档操作可以通过节点和位置抽象为多种子操作。例如，“Retain” （保持）表示在应用下一个操作之前要跳过文档中的多少位置。
Wave文档操作也支持annotation(注解)，注解是与节点和位置相关联的元数据，这对于描述文本格式特别有用，因为它不会使文档模型复杂化。示意图如下：

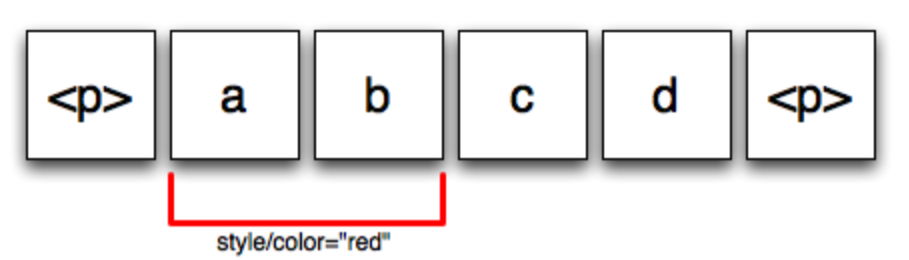
Wave文档操作可以抽象为以下子操作：

• retain
• insert characters
• insert element start
• insert element end
• delete characters
• delete element start
• delete element end
• replace attributes
• update attributes
• annotation boundary

3.转换函数

Wave 使用流接口表示文档操作，好处是可以简化操作转换为线性逻辑。操作转换的工作方式是将两个操作流作为输入，同时以线性方式处理并输出两个操作流，这种线性处理方式确保转换数量庞大的操作序列是高效的。示意图如下：

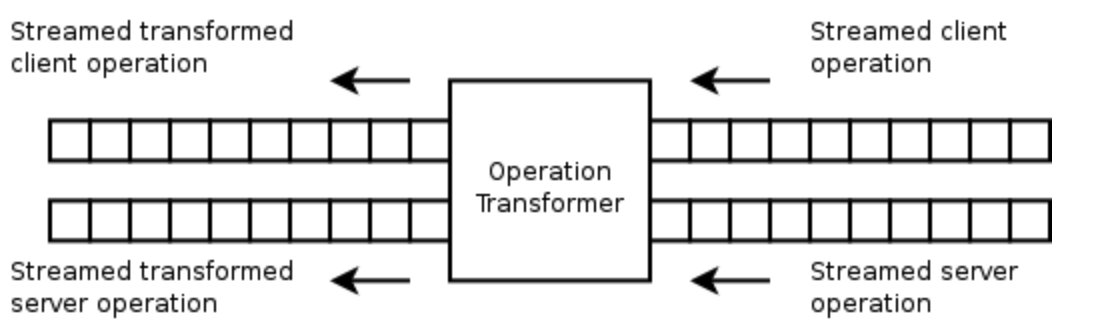
任意两个操作可以组合成一个新的操作，Wave的操作合成算法同样通过线性方式来高效处理，示意图如下：

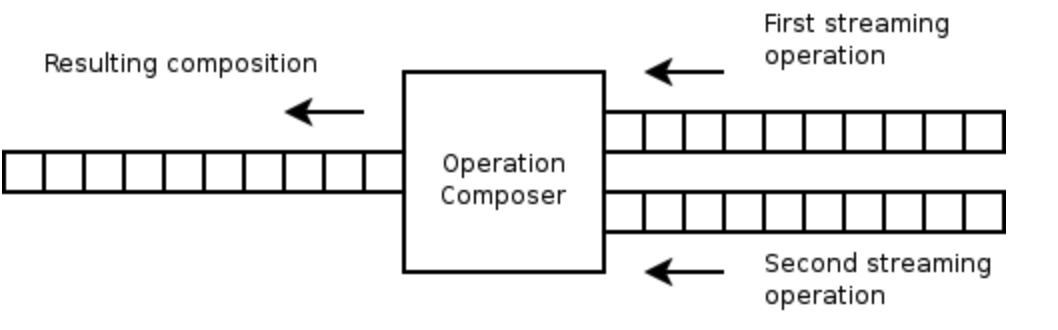
而当一个Wave客户端等待服务器确认的时候，客户端会组合它所有的缓存操作，这减少了需要发送和转换的操作数量。

4.客户端-服务端控制算法

拥有一个简单高效的服务端对于协同的可靠性和可扩展性非常重要。基于这个目标，Wave OT在原始OT的基础上，要求客户端在发送更多的操作之前等待服务器的确认。服务端确认客户端的操作意味着服务器已经转换了该客户端的操作，将其应用到服务端的副本上，并将转换后的操作广播给所有其他连接的客户端。当客户端在等待确认时，它会缓存本地产生的操作，之后将它们批量发送。通过增加确认逻辑，客户端可以推断出服务器的OT路径，这样客户端向服务器发送的操作可以保证始终在服务器的OT路径上，服务端只需要维护单个的状态空间（即应用的操作历史），当它接收到客户端的操作时，只需要根据操作历史记录转换操作，然后广播转换后的操作给其他客户端。通信协议的路径示意图如下所示，客户端的操作路径通过等待服务端的确认和转换，经过同步能获取到和服务端一致的结果：

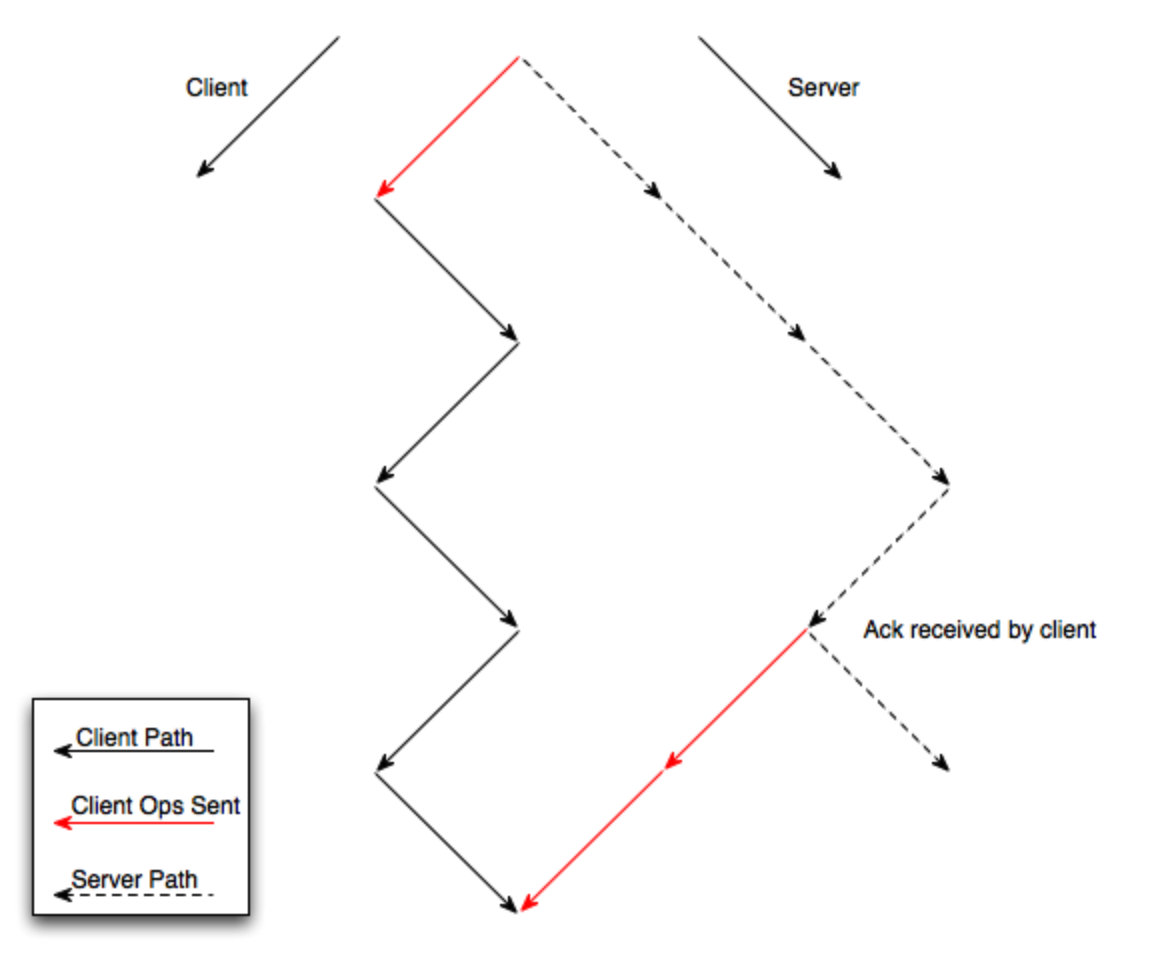
4.CRDT算法

4.1 简介

在分布式系统中，CRDT是一种能够在网络中多个主机间并行复制的数据结构，各个主机的副本可以独立且并行地更新而无需对各个副本进行协同，并且从数学角度可以解决所有可能的不一致问题。CRDT在2011年被首次正式定义后，文档协同编辑方面的应用也随之发展。CRDT同样也被应用到在线聊天系统、分布式数据库（如redis）等。

4.2 CRDT类型

CRDT一般分为两种类型，两种都可以实现数据的最终一致性：基于操作的CRDT和基于状态的CRDT。

• 基于操作的CRDT
  也被称作“复制交换数据类型”CmRDT，CmRDT副本只传播更新操作，其他副本在收到更新操作后会在本地进行合并和执行。CmRDT所有更新操作需要满足交换律，且需要服务端中间件保证传播的操作不会被删除或复制，也就是必须确保一个副本上的所有操作都要传播给其他副本，且必须没有重复项。

• 基于状态的CRDT
  也被称作“复制收敛数据类型”CvRDT，和CmRDT不同CvRDT会将副本的所有本地状态同步给其他副本，状态通过合并函数进行合并。合并函数必须是满足交换律、结合律和幂等律（解释见2.1节）的。状态的更新需要保持单调递增，为满足这一点更新操作必须按照偏序规则来执行。
  基于状态的CRDT通常更易于设计和实现，缺点是每个CRDT副本的整个状态最终都必须传输到其他副本，服务端开销很大；相比之下，基于操作的CRDT只传输更新操作，然而基于操作的CRDTs需要服务端中间件的保证操作的传播。

4.3 CRDT实现

4.3.1 G-Counter (Grow-only Counter)

G-counter是一个只增不减的计数器，对于N个节点，每个节点被分配一个从0到n-1范围的id。G-counter维护一个长度为N的数组P，每个节点都在数组中分配一个位置。更新操作后状态值增加并进行传播，更新函数内部状态单调递增，然后合并操作通过取数组P中的最大值来进行合并（即最新状态）。比较函数使状态满足偏序规则，而且合并函数满足交换律、结合律、幂等律。因此根据以上性质，G-Counter是一个能保证最终一致性的CvRDT。

伪代码如下：

payload integer[n] P     
    initial [0,0,...,0] 
update increment()     
    let g = myId()     
    P[g] := P[g] + 1 
query value() : integer v     
    let v = Σi P[i] 
compare (X, Y) : boolean b     
    let b = (∀i ∈ [0, n - 1] : X.P[i] ≤ Y.P[i]) 
merge (X, Y) : payload Z     
    let ∀i ∈ [0, n - 1] : Z.P[i] = max(X.P[i], Y.P[i])

由于CvRDT同步的是全量的状态，如果G-counter每个副本都单独进行累加，在进行合并时无法具体知道每个副本累加了多少。所以可行的方式是在每个副本上都使用一个数组保留其他副本的状态值，更新操作仅仅更新当前副本在数组中的对应项，合并时对数组每一项计算最大值进行合并，查询G-Counter结果即返回数组的和。

4.3.2 PN-Counter(Positive-Negative Counter)

CRDT发开中一个常见的策略是组合多个CRDT组成一个复杂的CRDT，PN-Counter即是由两个G-Counter组合起来的数据类型，既支持增也支持减操作。“P”G-Counter存放增操作的累加值，“N”G-Counter存放减操作的累加值。PN-Counter的值即是“P”G-Counter减去“N”G-Counter的值，合并函数就是分别合并两个P G-Counter和两个N G-Counter。伪代码如下：

payload integer[n] P, integer[n] N     
    initial [0,0,...,0], [0,0,...,0] 
update increment()     
    let g = myId()     
    P[g] := P[g] + 1 
update decrement()     
    let g = myId()     
    N[g] := N[g] + 1 
query value() : integer v     
    let v = Σi P[i] - Σi N[i] 
compare (X, Y) : boolean b     
    let b = (∀i ∈ [0, n - 1] : X.P[i] ≤ Y.P[i] ∧ ∀i ∈ [0, n - 1] : X.N[i] ≤ Y.N[i]) 
merge (X, Y) : payload Z     
    let ∀i ∈ [0, n - 1] : Z.P[i] = max(X.P[i], Y.P[i])     
    let ∀i ∈ [0, n - 1] : Z.N[i] = max(X.N[i], Y.N[i])

4.3.3 G-Set (Grow-only Set)

G-Set是一个只允许添加操作的集合，元素一旦添加就无法删除，两个G-set合并之后即为两个集合的并集。添加操作本质上是求并集，满足交换律、结合律、幂等律，满足CmRDT条件。伪代码如下：

payload set A     
    initial ∅ update add(element e)     
    A := A ∪ {e} 
query lookup(element e) : boolean b     
    let b = (e ∈ A) compare (S, T) : boolean b     
    let b = (S.A ⊆ T.A) 
merge (S, T) : payload U     
    let U.A = S.A ∪ T.A

4.3.4 2P-Set (Two-Phase Set)

类似PN-Counter，两个G-Set组合成一个2P-Set。增加一个删除集合（也称作“墓碑”集合），这样元素既可以被添加也可以被删除。元素一旦被删除就不能再次被添加，删除的元素会放到“墓碑”集合中；查询删除掉的元素将会返回false。2P-Set使用“remove-wins”策略，删除优先级高于添加。伪代码如下：

payload set A, set R     
    initial ∅, ∅ 
query lookup(element e) : boolean b     
    let b = (e ∈ A ∧ e ∉ R) 
update add(element e)     
    A := A ∪ {e} 
update remove(element e)     
    prelookup(e)     
    R := R ∪ {e} 
compare (S, T) : boolean b     
    let b = (S.A ⊆ T.A ∧ S.R ⊆ T.R) 
merge (S, T) : payload U     
    let U.A = S.A ∪ T.A     
    let U.R = S.R ∪ T.R

只同步操作，且两个集合只增不减，所以2P-Set为CmRDT。但2P-Set十分不实用，一方面已经删除的元素不能再次被添加，一方面删除的元素会保留在“墓碑”集合中，会占用大量空间。

4.3.5 LWW-Element-Set（Last-Write-Wins-Element-Set）

LWW-Element-Set和2P-Set类似，都由添加集合和删除集合组成，但每个被添加到集合的元素都会带上时间戳，同时删除元素元素被添加到“墓碑”集合也会带上最新的时间戳。如果元素在添加集合且不在“墓碑”集合中，或者元素同时在两个集合中但“墓碑”集合中所带的时间戳早于添加集合中的时间戳，则此元素是LWW-Element-Set的成员。合并LWW-Element-Set的两个副本，同样是两种集合分开合并，当元素时间戳相同时，可以通过偏向规则偏向于添加或删除。LWW-Element-Set相比于2P-Set，允许同一元素被删除后再次添加。

4.3.6 OR-Set (Observed-Remove Set)

OR-Set类似LWW-Element-Set，但使用唯一的tag标记代替了时间戳。集合中的每个元素都维护一个添加标记列表(add-tag list)和一个删除标记列表(remove-tag list)，元素添加到集合则会生成一个唯一tag标记并添加到元素对应的add-tag list，删除元素则是将元素add-tag list中的所有标记都添加到remove-tag list。合并两个OR-Set时，会将每个元素的add-tag list和remove-tag list同时分开合并。当且仅当add-tag list比remove-tag list小，且列表非空时，对应的元素才属于OR-Set的成员。通过对每个副本维护一个时间戳向量可以很容易地对OR-Set进行优化，这样即可以废弃remove-tag list, 避免了潜在的无限增长占用大量空间。

4.3.7 Sequence CRDTs

以上介绍的CRDT更多地用在分布式数据库等领域，而实时协同编辑领域主要应用序列、列表或有序集的CRDT，称作Sequence CRDT。比较名声在外的Sequence CRDT算法，比如：Treedoc、RGA、WOOT等。实际应用中，Yjs框架提供类似Map、Array等Sequence CRDT支持文档实时协同编辑，Nimbus Note即是使用的Yjs框架来实现协同编辑；Atom编辑器的teletype插件则是使用WOOT算法来实现协同编辑；微软的Fluid Framework也提供SharedString、Matrix等Sequence CRDT用来实现协同。

这里简单介绍下Atom-teletype使用的WOOT算法，如何利用CRDT保证文档最终一致性：

WOOT算法中，定义操作按阶段顺序分为三种：生成操作、接受操作、集成操作。

1.生成操作
生成插入操作伪代码如下：

GenerateIns(pos, α)
    Hs:=Hs+ 1
    let cp:=ithVisible(strings, pos),
        cn:=ithVisible(strings, pos+ 1),
        wchar:=<(numSites, Hs), α, True, cp.id, cn.id >
    IntegrateIns(wchar, cp, cn)
    broadcastins(wchar)

生成插入逻辑大致如下：
1.把本地时钟的值+1（时钟是用来分辨同一客户端下两个操作的先后关系的，后续会用作ID的大小比较）。
2.找出执行插入的位置对应的节点的前置和后置依赖节点（如果节点不可见，则会继续遍历直至找到可见节点）。
3.本地集成插入操作。
4.广播该插入操作。

生成删除操作伪代码如下：

GenerateDel(pos)
    let wchar:=ithVisible(strings, pos)
    IntegrateDel(wchar)
    broadcastdel(wchar)

生成删除则是检查该位置是否可见，然后本地集成并广播删除操作。

2. 接受操作
判断操作是否可接受函数伪代码如下：

isExecutable(op)
    let c:=char(op)
    if type(op) =del then 
        return contains(strings, c)
    else
        return contains(strings, CP(c)) 
        and contains(strings, CN(c))
    endif

伪代码逻辑简单理解为：
1.对于删除操作，待删除字符c必须存在于字符串内
2.对于插入操作，字符串内必须存在待插入字符的前置依赖节点CP和后置依赖节点CN
另外因为不同站点同步的操作无法保证先后顺序和因果关系，所以需要维护一个操作池保存挂起的操作。伪代码如下：

Reception(op)
    add op to pool

整个循环集成的过程是不断从操作池取出可接受执行的操作进行集成，伪代码如下：

Main()
    loop
        find op in pools such that isExecutable(op) 
        let c:=char(op)
        if type(op) =del then 
            IntegrateDel(c)
        else 
            IntegrateIns(c, CP(c), CN(c)) 
        endif
    endloop

3.集成操作
集成插入操作伪代码如下：

// c：实际需要插入的字符，cp:依赖的前置字符，cn: 依赖的后置字符
IntegrateIns(c, cp, cn)
    let S:=strings                 // S:完整字符串
    let S′:=subseq(S, cp, cn)      // cp和cn中间截取的字符串
    if S′=∅ then
        insert(S, c, pos(S, cn))   // S'为空，则在cp和cn之间位置插入字符c
    else
    // L是S'的复制，但删除了在S'中包含的前置和后置字符
    let L:=cp d0d1. . . dmcn where d0. . . dm are the W−char in            S′ such that CP(di)≤cp and cn≤CN(di)
    let i:= 1
    while(i <|L|−1) and (L[i]<idc)do
        i:=i+ 1
    endwhile
    IntegrateIns(c,L[i−1],L[i])
endif

集成插入操作逻辑大致上是以下几步：
(1)声明每个节点应有的前置和后置依赖节点
(2)截取出待插入字符依赖的前置和后置节点之间的字符串
(3)遍历截取的字符串，去除前置或后置节点在这个字符串中的字符
(4)遍历得到的字符串，找到最后一个ID比待插入字符小的字符对应的位置，在此处执行插入

集成删除操作伪代码如下：

IntegrateDel(c)
    c.v:=False

删除操作比较简单，将对应字符节点设置为不可见。

下面看一个处理协同冲突的简单例子：

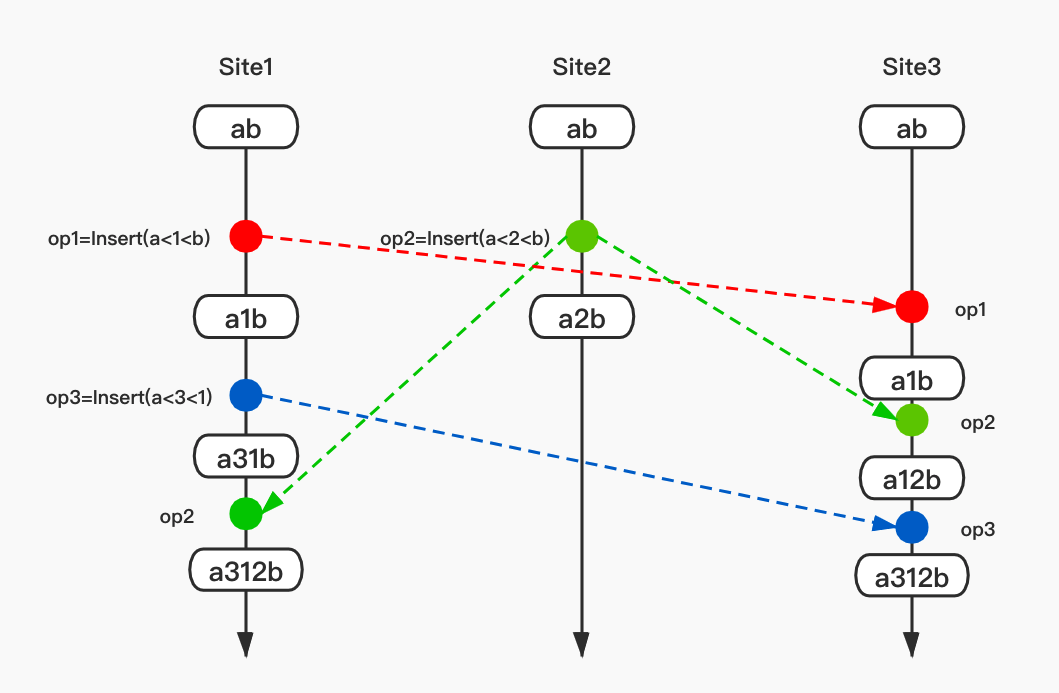
如上图，op2同步到site3进行集成时，site3本地的文本字符串是"a1b"，字符节点2和字符节点1进行ID比较，字符1的ID小于字符2的ID，所以插入之后字符串变为“a12b”, 之后集成op3，直接在a和1之间插入；在site1集成op2时，比较1和2字符的ID，同样插入2在1之后，这样保证了三个客户端最终的结果一致性。
Atom-teletype底层引入了数据结构ID Tree，用来维护节点的ID保证查询和插入效率，具体实现本文不做赘述。

5.AST算法

 AST的基本存储结构为线性结构，AST需要管理的是一系列操作的集合，然后将这些操作确定一个全序关系。这样不管操作在每个站点的到达顺序是怎么样的，都会按照一个确定的顺序执行并且使得每个站点得到的文档状态最终一致。

5.1 状态向量

给操作排序，需要给每个操作增加时间戳数据，由于每个站点的时间不一定一致，所以应用状态向量（时间戳向量）来解决。
N表示协同编辑站点的个数，每个站点都有一个唯一的ID，然后对于这些ID从1-N编号，这样每个协同站点都会维护一个N维的状态向量TS，状态向量的分量值TS[i]表示站点i本地操作执行的次数（即状态更新的次数）。各站点执行操作后状态向量的变化如下图：

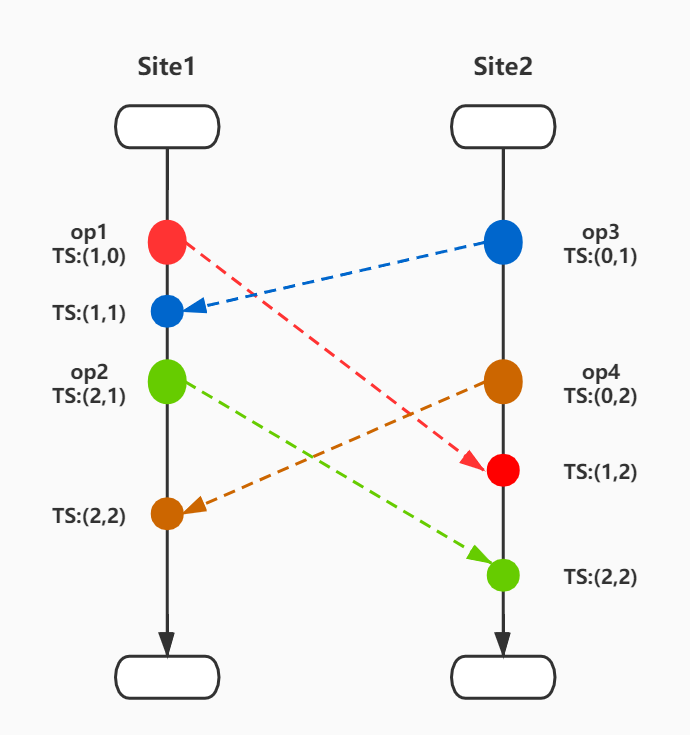
对上图做简单解释：两个协同站点Site1和Site2，因此每个站点维护一个2维状态向量TS，状态向量初始值均为TS:(0,0)。对于SIte1来说，op1执行后状态向量更新为(1,0)，之后获取到Site2同步op3，则状态向量更新为(1,1) 表示两个站点状态均更新一次，之后Site1本地执行op2状态向量更新为(2,1)，然后接收到Site2同步的op4，状态向量最终更新为(2,2)；Site2同上。

状态向量的大小关系

两个状态向量a，b 若a=b则a和b的每个分量都相等。若a<b则a中每个分量都小于等于b中的对应分量，且至少有一个分量小于对应分量。若a>b则a中至少有一个分量大于b中的对应分量。
举个例子 ：(0,0,0) < (1,0,1) < (1,1,1) = (1,1,1)
定义[op, TS]为操作的传输结构，其中op表示插入和删除两种基本操作之一，而TS表示状态向量。

5.2 地址空间转换

在协同编辑算法中，操作被分为两种：本地操作和远程操作。为了保证良好的用户体验，操作产生或者被接收会直接在站点上执行，然而为了保证每个站点副本内容的一致性，操作必须有序的执行。综合考虑两点矛盾就产生了，如果远程操作到达的顺序和产生的顺序相反那么后到来的操作如何执行呢？AST的解决方案很简单，通过地址空间转换回到操作产生时的文本状态执行该操作，也就是说在执行一个远程操作之前先消除应该在该操作之后执行的操作对于文本的影响，在此远程操作执行完之后再恢复那些操作的影响。
地址空间由若干节点组成，每个节点除了字符信息外还有一个有效位（节点是否有效，在回溯操作中需要用到），另外节点上包含对于这个字符基本操作和状态向量两部分。地址空间结构如下图所示：

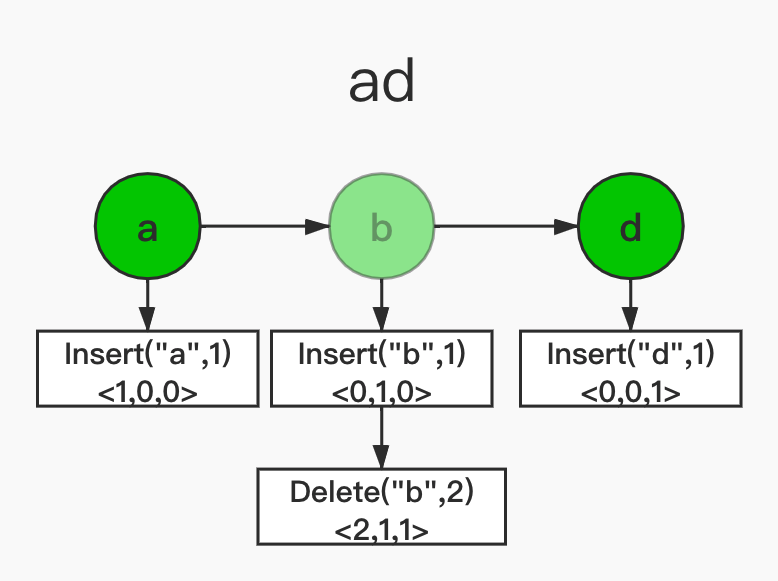
地址空间结构图（半透明为无效节点）

5.3 回溯算法

文本执行时状态指的是因果先序操作集合，因此在地址空间回溯的时候应该仅仅保留因果先序操作集合。

回溯算法

性质1：一个操作可以在站点上执行当且仅当以下两种情况：
(1)操作是该站点的本地操作
(2)操作是远程操作且操作的因果先序操作已经在当前站点上全部执行结束。

性质2：定义操作A和操作B的状态向量分别为SVa和SVb，若A->B 因果先序, 则有SVa<SVb
; A||B 并发关系, 则有SVa>SVb && SVb>SVa; B->A 因果后序,则有SVb<SVa

根据性质1、2可以设计回溯算法基本框架，回溯算法伪代码如下：

逻辑流程大致如下：对于每个操作节点进行扫描，通过状态的比较判断此操作是否为当前操作的因果先序操作，若是则将操作节点置为有效，否则置为无效。回溯算法的目的是回到操作产生时的文本状态，也就是仅仅保留因果先序操作。

5.4 控制算法

来自R站点的远程操作O所带状态向量为SVo，且操作满足性质1，在S站点本地当前状态向量为SVs,在S站点本地集成远程操作O对应控制算法伪代码如下：

逻辑流程大致如下：首先回溯到操作O产生时的文本状态，然后执行操作O并加入状态向量到字符节点，接着更新当前S站点状态，最后回溯S站点到当前状态，将地址空间恢复到包含了新操作执行效果。
一个具体的例子如下图所示：

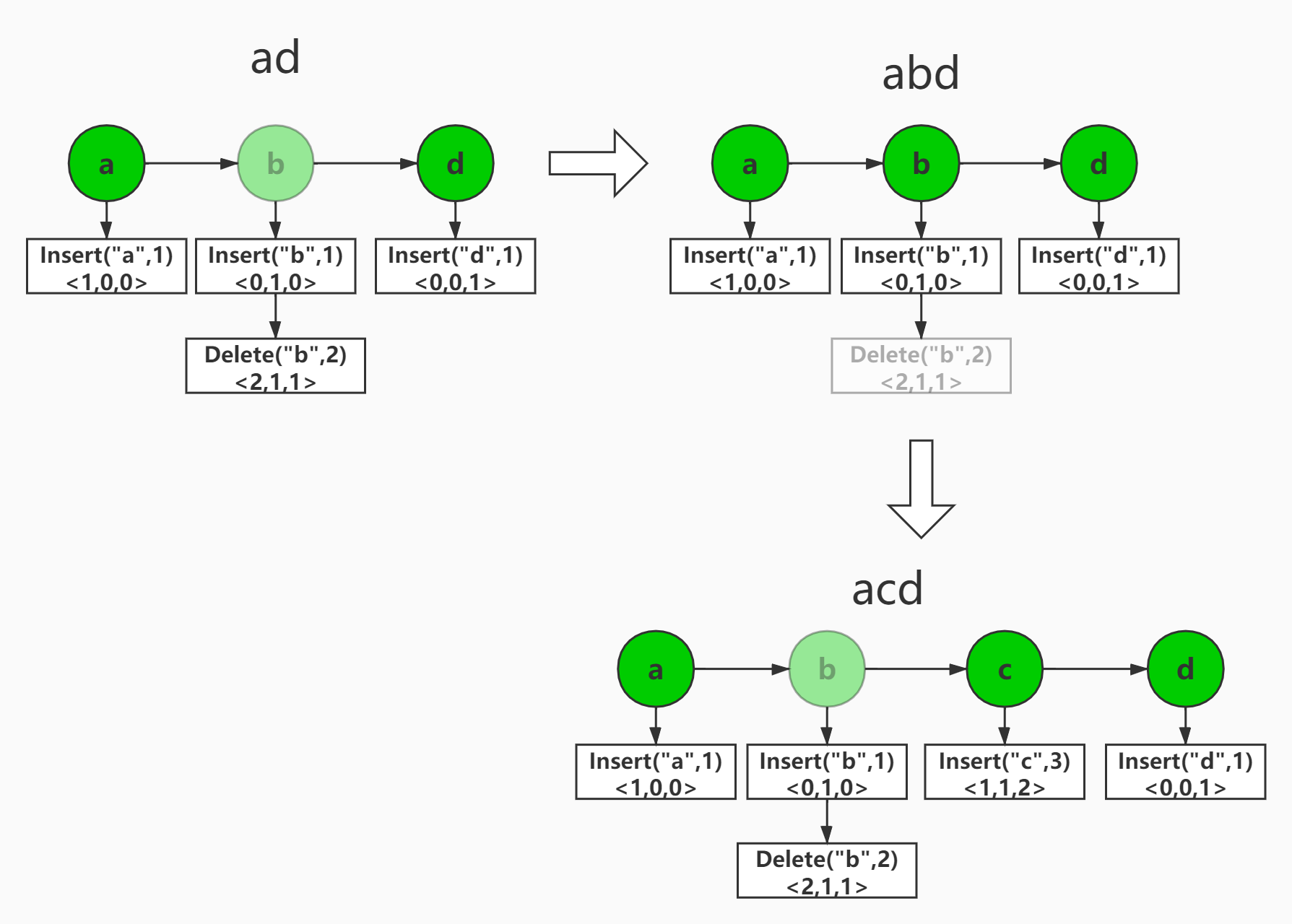
基于文本执行操作Insert["c", 3],状态向量为<1,1,2>，则执行顺序为首先通过控制算法将文本状态回溯到状态<1,1,2>之前，此时操作Delete["b",2]执行效果会失效，然后执行Insert["c",3]之后本地状态向量会更新为<2,1,2>,最后执行回溯算法则Delete["b",2]生效且保留了Insert["c",3]的执行效果。

5.5 操作执行算法

若操作O是一个删除操作，则仅需在地址空间中找到操作的相应位置（从左至右对有效节点计数），将操作添加到这个节点上。
若操作O是一个插入操作，在地址空间中找到操作的相应位置（从左至右对有效节点计数），建立一个新的字符节点，初始化节点的标记并把它插入到插入范围中的一个确定位置。
对于插入操作存在一个问题：根据插入操作的位置仅仅能够确认插入的位置位于两个有效节点之间，但并不能够知道具体位置（两个有效节点之间可能存在若干个无效节点）。
对于这个问题AST是通过range-scan算法来确定操作的具体插入位置，range-scan的原理在于通过定义TOrder函数来确定操作两两之间的全序关系。TOrder函数的定义如下：
两个字符节点CNa和CNb，对应操作的状态向量为SVa和SVb，存在TOrder(CNa) < TOrder(CNb)当且仅当满足两种情况：
(1)sum(SVa)<sum(SVb)
(2)sum(SVa)=sum(SVb)且a<b
TOrder是一个全序关系且是传递的，也就是说任意两个节点之间是可比较的。在这个基础上提出了range-scan算法（CNa和CNb是算法的执行范围，是两个相邻的有效节点（依赖的前置和后置节点），CNnew是将要插入的节点，P表示一个位置）：

逻辑流程大致如下：首先将两个有效节点之间的节点分为两类：因果先序操作节点（算法12-17行）和并发关系操作节点（算法4-11行）。外层循环依次扫描每个节点直到遇到有效节点或CNb停止，并返回对应位置。对于因果先序操作节点规定新节点一定插入在其右侧，对于并发关系操作节点则按照TOrder函数比较插入在合适的位置。
回溯过程将插入定位到一个确定的范围内。range-scan为这个插入在范围中确定一个唯一的位置，并使其不受并发操作的影响。

6.总结

OT算法的主要思想是本地产生的操作立刻执行, 接收到的远程操作需要进行操作转换后再执行。与传统的锁机制和串行化方法相比, OT算法的优势是具有很好的本地响应，但OT算法也面临一些技术挑战，例如设计正确的操作转换函数比较复杂、不断发现特定协同场景下存在“puzzle”、大部分OT算法伸缩性不足等。尽管如此OT算法作为最早提出的协同编辑冲突处理算法，在现实中得到了非常广泛的实际应用。
AST算法在处理远程操作时，是通过计算文档地址空间将文档状态回退到操作产生时的状态来获取操作执行的正确位置。基于AST各种相关算法被提出用于解决一些协同编辑的特定问题。
CRDT算法声称不需要保存操作历史，并发操作之间不需要进行操作转换，使得CRDT算法具有很好的伸缩性，适用于大规模的p2p协同编辑领域。CRDT算法同样面临一些技术挑战，例如设计并发操作的可交换执行相对复杂、需要考虑如何减少操作ID的空间开销等。

参考文献：

[1] D. Sun and S. Xia and C. Sun and D. Chen (2004). "Operational transformation for collaborative word processing". Proc. of the ACM Conf. on Computer-Supported Cooperative Work. pp. 437–446.
[2] Claudia-Lavinia Ignat; Moira C. Norrie (2008). "Multi-level Editing of Hierarchical Documents". Computer Supported Cooperative Work (CSCW). 17 (5–6): 423–468. 
[3] Gu N, Yang J, Zhang Q. Consistency maintenance based on the mark & retrace technique in groupware systems[C]// Proceedings of the 2005 International ACM SIGGROUP Conference on Supporting Group Work, GROUP 2005, Sanibel Island, Florida, USA, November 6-9, 2005. 2005:264-273.
[4] Oster G, Urso P, Molli P, et al. Data consistency for P2P collaborative editing[C]//Proceedings of the 2006 20th anniversary conference on Computer supported cooperative work. 2006: 259-268.
[5] Zhang J, Lu T, Xia H, et al. ASTS: A string-wise address space transformation algorithm for real-time collaborative editing[C]//2017 IEEE 21st International Conference on Computer Supported Cooperative Work in Design (CSCWD). IEEE, 2017: 162-167.
[6] Nédelec B, Molli P, Mostefaoui A, et al. LSEQ: an adaptive structure for sequences in distributed collaborative editing[C]//Proceedings of the 2013 ACM symposium on Document engineering. 2013: 37-46.